![Hur Linux byggs och utvecklas [Video]](https://gadget-info.com/img/how/761/how-linux-is-built-developed.jpg)
I motsats till detta, i fallet med en kombination, spelar ingen roll alls. Inte bara i matematik utan även i det praktiska livet går vi regelbundet igenom dessa båda begrepp. Även om vi märker det aldrig. Så läs igenom artikeln noga, för att veta hur dessa två begrepp är olika.
Jämförelsediagram
| Grunder för jämförelse | Permutation | Kombination |
|---|---|---|
| Menande | Permutation hänvisar till de olika sätten att ordna en uppsättning objekt i en sekventiell ordning. | Kombinationen hänvisar till flera sätt att välja objekt från en stor uppsättning objekt, så att deras ordning inte spelar någon roll. |
| Ordning | Relevant | Irrelevant |
| betecknar | Arrangemang | Urval |
| Vad är det? | Beställda element | Oordnade uppsättningar |
| svar | Hur många olika arrangemang kan skapas från en viss uppsättning objekt? | Hur många olika grupper kan väljas från en större grupp av objekt? |
| Härledning | Multipla permutation från en enda kombination. | Enkel kombination från en enda permutation. |
Definition av permutation
Vi definierar permutation som olika sätt att ordna några eller alla medlemmar i en uppsättning i en viss ordning. Det innebär all möjlig ordning eller omplacering av den givna uppsättningen, i särskild ordning.
Till exempel, All möjlig permutation skapad med bokstäver x, y, z -
- Genom att ta alla tre i taget är xyz, xzy, yxz, yzx, zxy, zyx.
- Genom att ta två i taget är xy, xz, yx, yz, zx, zy.
Totalt antal möjliga permutationer av n saker som tas r i taget kan beräknas som:
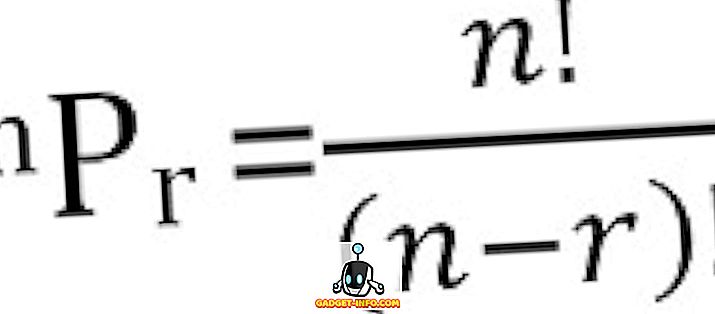
Definition av kombination
Kombinationen definieras som olika sätt att välja en grupp genom att ta några eller alla medlemmar i en uppsättning utan följande ordning.
Till exempel, Alla möjliga kombinationer som valts med bokstaven m, n, o -
- När tre av tre bokstäver ska väljas är den enda kombinationen mno
- När två av tre bokstäver ska väljas är de möjliga kombinationerna mn, nej, om.
Totalt antal möjliga kombinationer av n saker som tas r vid en tidpunkt kan beräknas som:
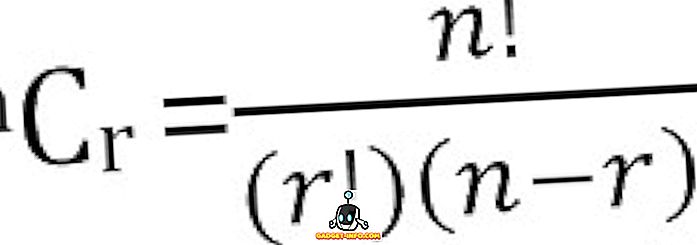
Viktiga skillnader mellan permutation och kombination
Skillnaderna mellan permutation och kombination är tydliga på följande grunder:
- Termen permutation hänvisar till flera sätt att ordna en uppsättning objekt i en sekventiell ordning. Kombination innebär flera sätt att välja objekt från en stor pool av objekt, så att deras order är irrelevant.
- Den primära skillnaden mellan dessa två matematiska begrepp är order, placering och position, dvs i permutationsegenskaper som nämns ovan spelar ingen roll, vilket spelar ingen roll vid kombinationen.
- Permutation anger flera sätt att ordna saker, personer, siffror, alfabet, färger etc. Å andra sidan anger kombinationen olika sätt att välja menyalternativ, mat, kläder, ämnen, etc.
- Permutationen är ingenting annat än en ordnad kombination, medan kombination innebär att orättvisa uppsättningar eller parning av värden inom specifika kriterier.
- Många permutationer kan härledas från en enda kombination. Omvänt kan endast en enda kombination erhållas från en enda permutation.
- Permutation svar Hur många olika arrangemang kan skapas från en viss uppsättning objekt? I motsats till kombinationen som förklarar Hur många olika grupper kan plockas från en större grupp av objekt?
Exempel
Antag att det finns en situation där du måste ta reda på det totala antalet möjliga prover av två av tre objekt A, B, C. I den här frågan måste du först och främst förstå huruvida frågan är relaterad till permutation eller kombination och det enda sättet att ta reda på det här är att kontrollera om ordern är viktig eller inte.
Om ordern är signifikant är frågan relaterad till permutation, och eventuella prover kommer att vara, AB, BA, BC, CB, AC, CA. Var, AB skiljer sig från BA, BC skiljer sig från CB och AC är annorlunda CA.
Om ordern är irrelevant är frågan relaterad till kombinationen, och eventuella prover kommer att vara AB, BC och CA.
Slutsats
Med ovanstående diskussion är det tydligt att permutation och kombination är olika termer, vilka används i matematik, statistik, forskning och vårt dagliga liv. En sak att komma ihåg, om dessa två begrepp är att för en given uppsättning objekt kommer permutationen alltid att vara högre än dess kombination.
