Till skillnad från standardavvikelsen är kvadratroten av det numeriska värdet som erhållits vid beräkning av variansen. Många människor kontrasterar dessa två matematiska begrepp. Så, med denna artikel försöker man kasta ljus på den viktiga skillnaden mellan varians och standardavvikelse.
Jämförelsediagram
| Grunder för jämförelse | Variation | Standardavvikelse |
|---|---|---|
| Menande | Varians är ett numeriskt värde som beskriver variationen i observationer från dess aritmetiska medelvärde. | Standardavvikelse är ett mått på spridning av observationer inom en dataset. |
| Vad är det? | Det är genomsnittet av kvadratiska avvikelser. | Det är roten medelvärde kvadratisk avvikelse. |
| Märkt som | Sigma-kvadrerade (σ ^ 2) | Sigma (σ) |
| Uttryckt i | Kvadrerade enheter | Samma enheter som värdena i datamängden. |
| Pekar på | Hur långt individer i en grupp sprids ut. | Hur mycket observationer av en dataset skiljer sig från dess medelvärde. |
Definition av varians
I statistik definieras varians som måttet på variabilitet som representerar hur långt medlemmar i en grupp sprids ut. Det finner ut den genomsnittliga graden som varje observation varierar från medelvärdet. När variansen hos en dataset är liten visar den datapunkternas närhet till medelvärdet medan ett större värde av varians representerar att observationerna är mycket dispergerade kring det aritmetiska medelvärdet och från varandra.
För oklassificerad data :
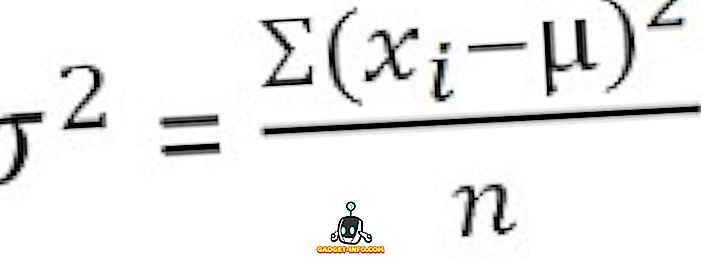
För grupperad frekvensfördelning :
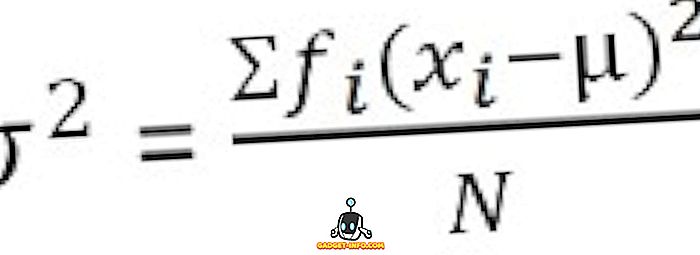
Definition av standardavvikelse
Standardavvikelse är ett mått som kvantifierar mängden dispersion av observationerna i en dataset. Den låga standardavvikelsen är en indikator på närhet av poängen till det aritmetiska medelvärdet och en hög standardavvikelse representerar; poängen sprids över ett högre värdeområde.
För oklassificerad data :

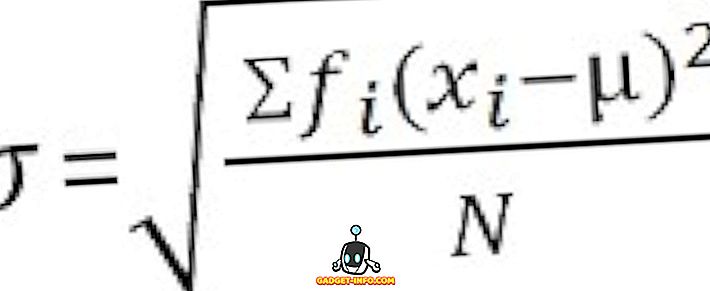
Viktiga skillnader mellan variation och standardavvikelse
Skillnaden mellan standardavvikelse och varians kan dras tydligt av följande skäl:
- Varians är ett numeriskt värde som beskriver variationen i observationer från dess aritmetiska medelvärde. Standardavvikelse är ett mått på spridning av observationer inom en dataset.
- Variansen är inget annat än ett genomsnitt av kvadratiska avvikelser. Å andra sidan är standardavvikelsen roten medelvärde kvadratisk avvikelse.
- Varians betecknas med sigma-kvadrat (σ2), medan standardavvikelsen är märkt som sigma (σ).
- Variansen uttrycks i kvadratiska enheter som vanligtvis är större än värdena i den givna datasatsen. I motsats till standardavvikelsen som uttrycks i samma enheter som värdena i uppsättningen data.
- Variansen mäter hur långt individer i en grupp sprids ut. Omvänt mäter Standardavvikelse hur mycket observationer av en datamängd som skiljer sig från dess medelvärde.
Illustration
Studerade poäng av en student i fem ämnen är 60, 75, 46, 58 respektive 80. Du måste ta reda på standardavvikelsen och variansen.
Först och främst måste du ta reda på den genomsnittliga,

Så genomsnittet (medelvärdet) är 63, 8
Beräkna nu variansen
| X | en | (XA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63, 8 | -3, 8 | 14, 44 |
| 75 | 63, 8 | 11, 2 | 125, 44 |
| 46 | 63, 8 | -17, 8 | 316, 84 |
| 58 | 63, 8 | 5, 8 | 33, 64 |
| 80 | 63, 8 | 16, 2 | 262, 44 |
Var, X = Observationer
A = Aritmetisk medelvärde
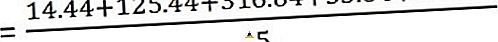
Och standardavvikelsen är -

Likheter
- Både varians och standardavvikelse är alltid positiva.
- Om alla observationer i en dataset är identiska kommer standardavvikelsen och variansen att vara noll.
Slutsats
Dessa två är grundläggande statistiska termer, som spelar en viktig roll i olika sektorer. Standardavvikelsen är föredragen över genomsnittet eftersom den uttrycks i samma enheter som mätningarna medan variansen uttrycks i enheterna större än den givna datasatsen.